스칼라곱?

예제1)

예제2) 코시-슈바르츠 부등식을 증명하여라

'[전공수학] 이론 > 미분기하학' 카테고리의 다른 글
| 직교화 (0) | 2020.10.21 |
|---|---|
| 기저 (0) | 2020.10.02 |
| 일차종속, 일차독립 (0) | 2020.10.02 |
스칼라곱?

예제1)

예제2) 코시-슈바르츠 부등식을 증명하여라

| 직교화 (0) | 2020.10.21 |
|---|---|
| 기저 (0) | 2020.10.02 |
| 일차종속, 일차독립 (0) | 2020.10.02 |
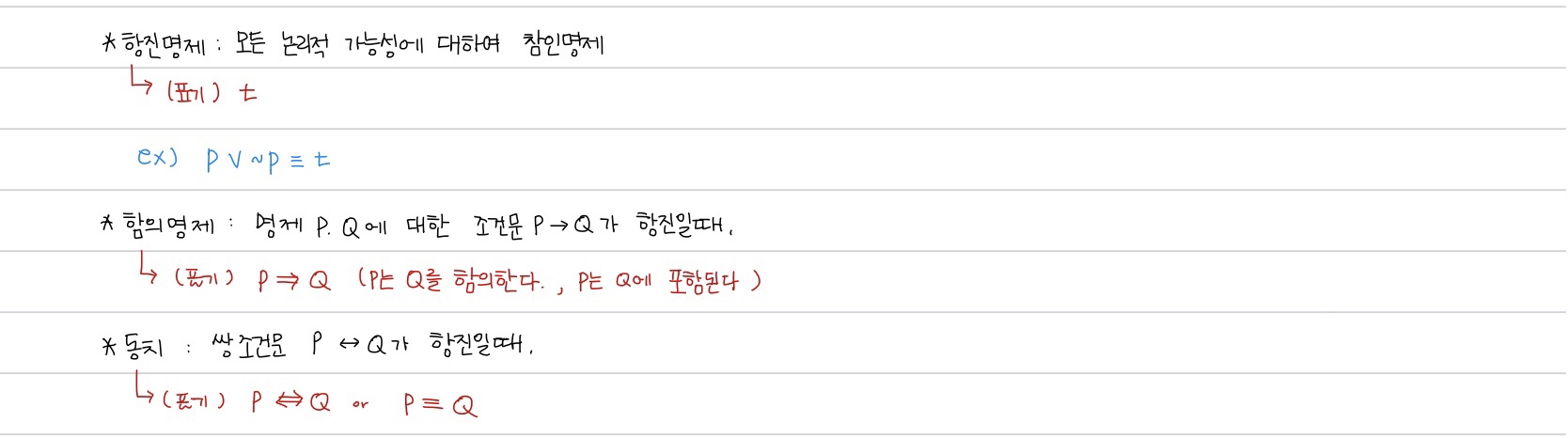
항진명제, 함의명제, 동치, 모순?

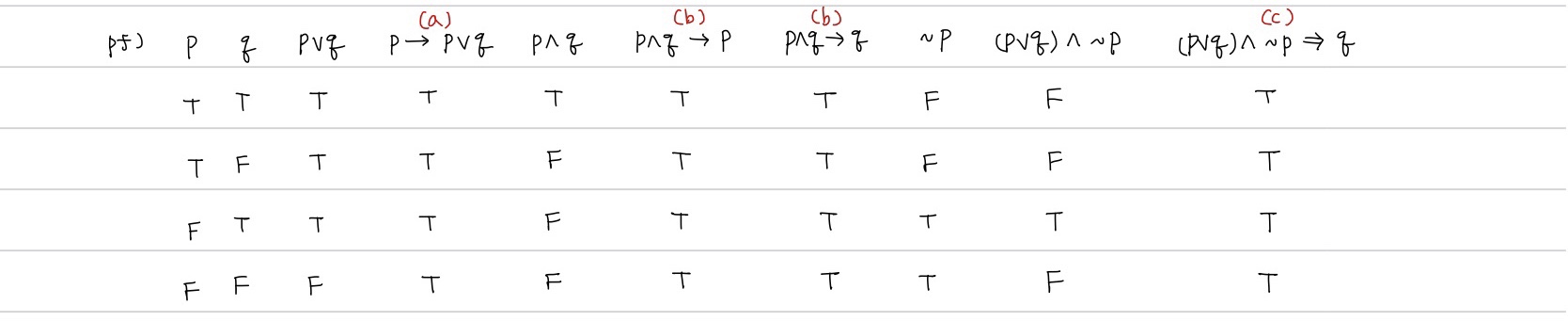
Thm1) (합의법칙, 단순화법칙, 논리합의 삼단논법)

Pf)
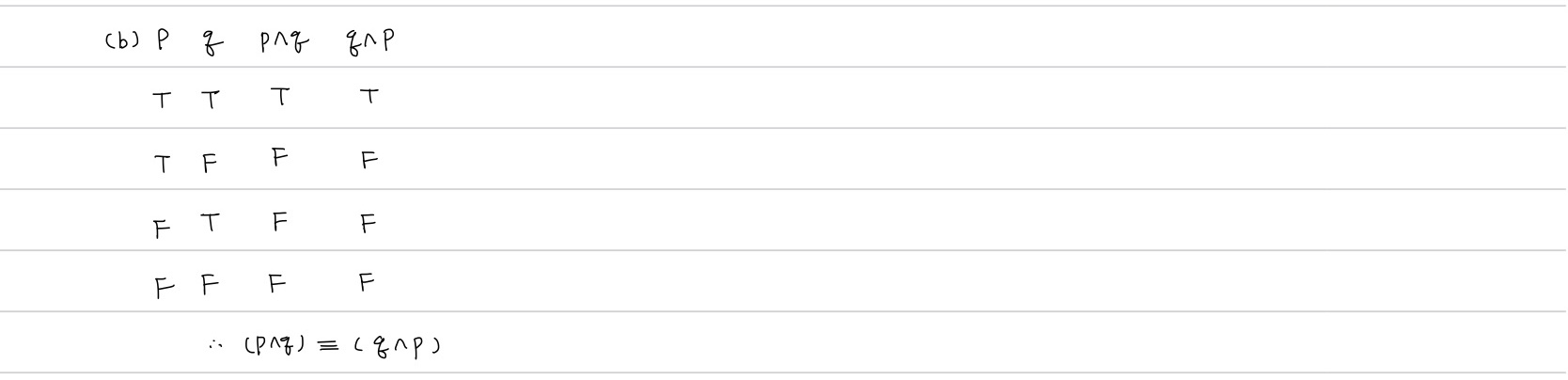
Thm2) (이중부정법칙, 교환법칙, 멱등법칙, 대우법칙)

Pf)




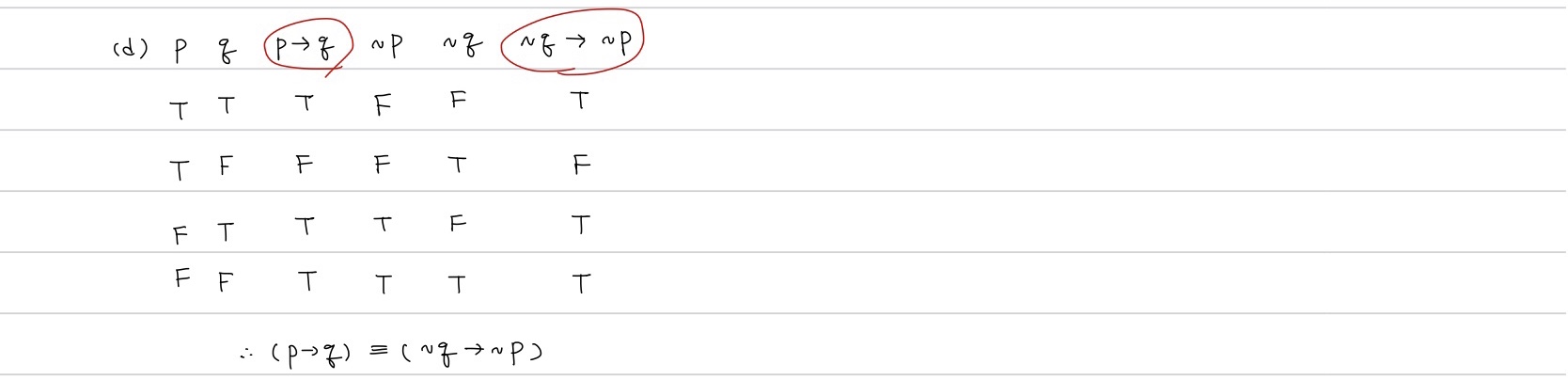
Thm3) (드모르간의 법칙)

Pf)

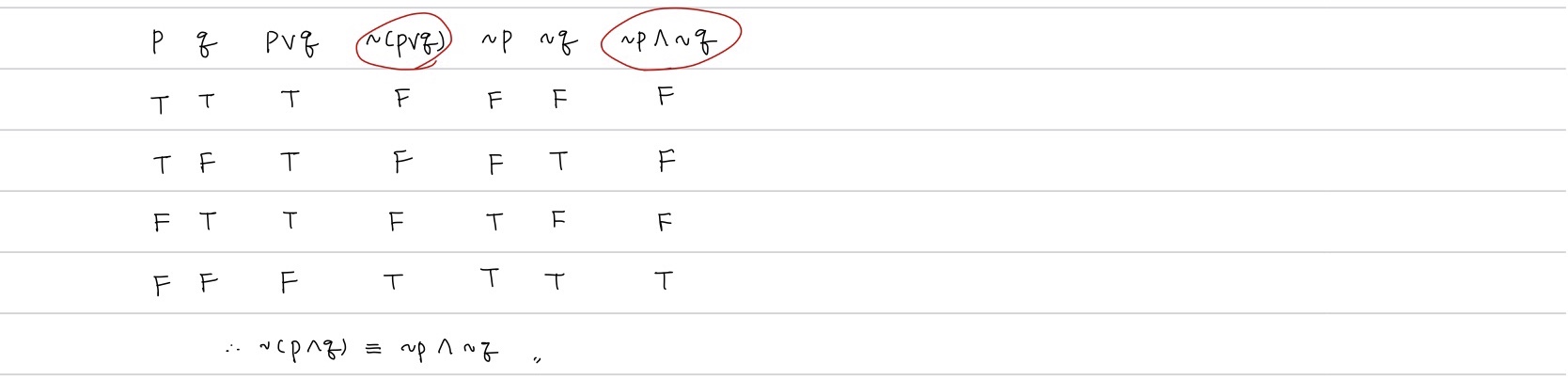
Thm4) (결합법칙, 분배법칙, 추이법칙)
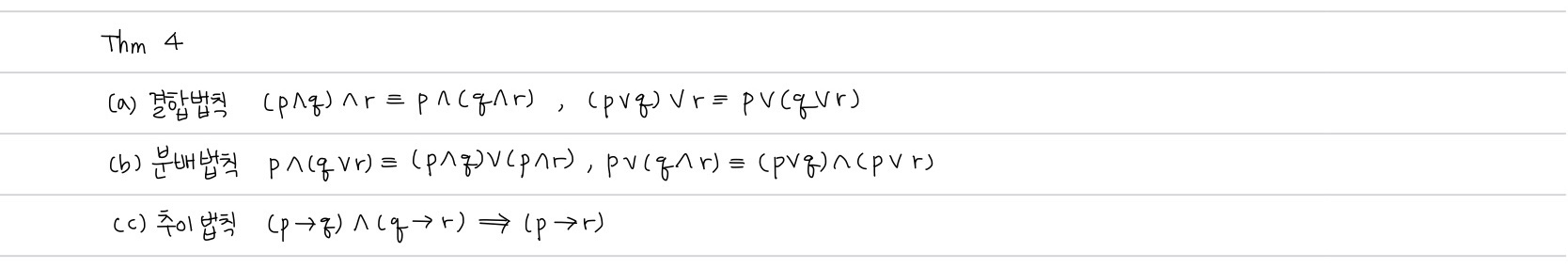
Pf)


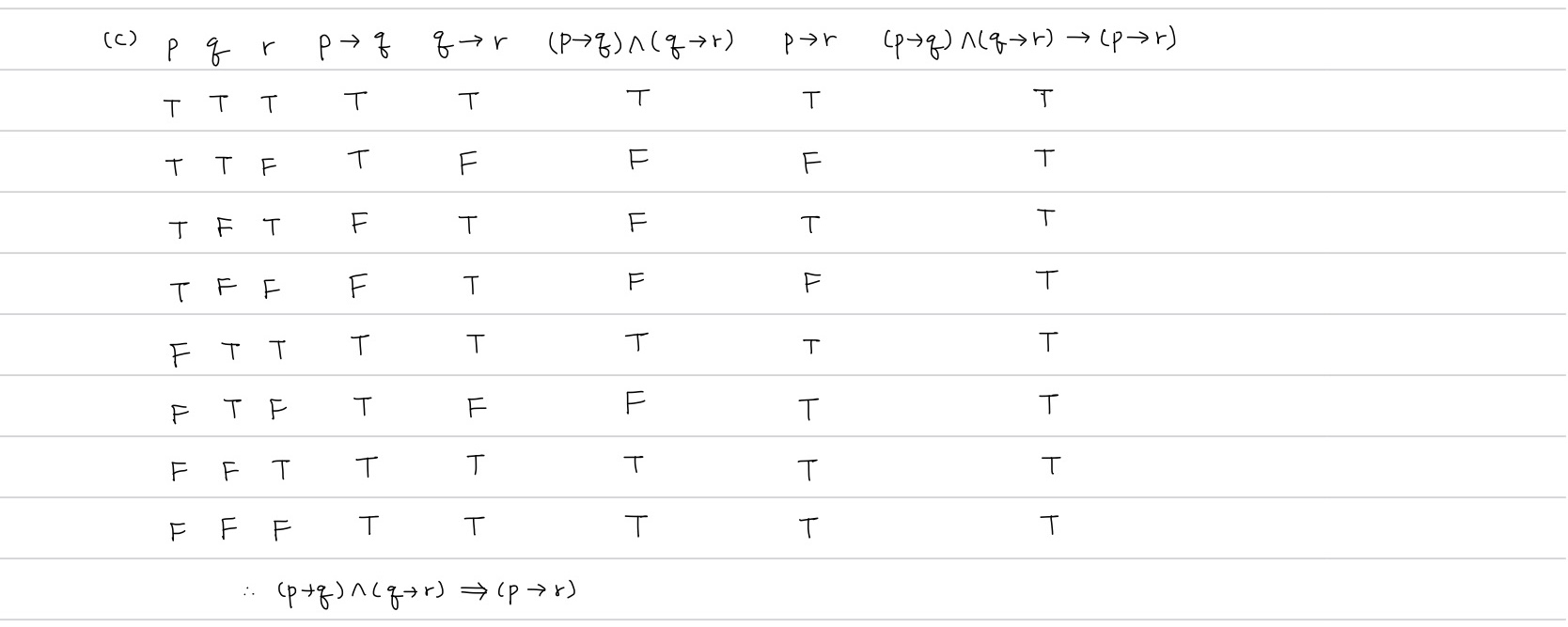
Thm5) (구성적 양도논법, 파괴적 양도논법)

Thm6) (긍정식 삼단논법, 부정식 삼단논법, 귀류법, 배리법)

Pf)

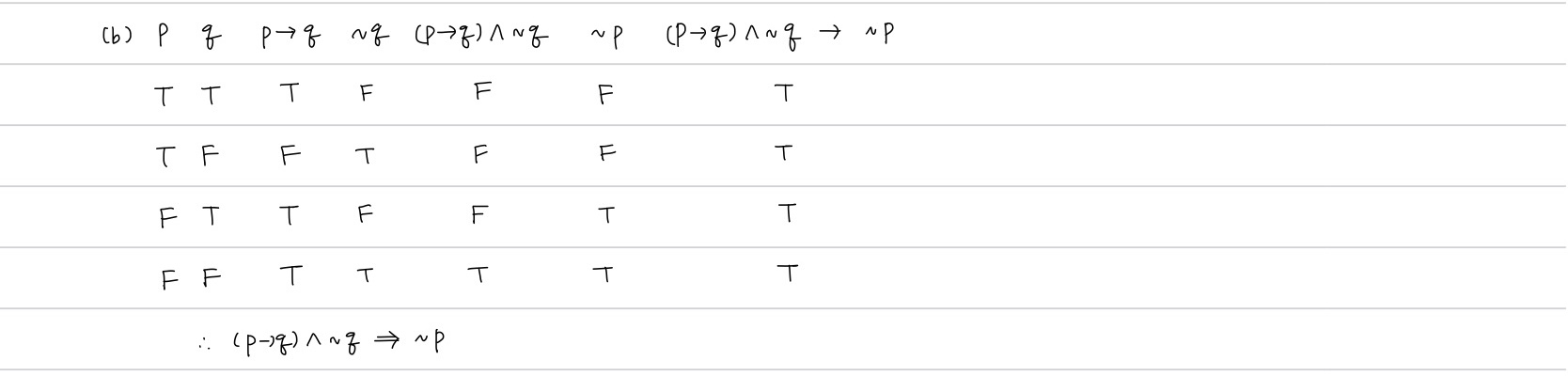

Thm7) (항진명제, 모순명제 관련성질)

Pf)



명제란?

단순명제들을 결합하여 합성명제를 구성하는 방법으로 다섯가지의 결합자들이 이용되고 있다.

명제p, q의 참, 거짓과 그 결합자에 의해 합성명제의 참거짓이 결정되는데
그 참, 거짓을 다음과 같은 진리표에 실어두면 편리하다.

Q1) 논리합, 조건문, 쌍조건문의 동치관계를 진리표를 이용하여 증명하여라

| 유한집합 무한집합 (0) | 2020.12.12 |
|---|---|
| 초등논리와 여러가지 성질들 (0) | 2020.10.11 |
*기저
집합 $B$가 $ E^{3} $의 기저가 되려면
i) 집합 $B$의 모든 벡터는 일차독립
ii) $E^{3}$의 모든 벡터가 집합 $B$의 일차결합으로 표시가능
(note1) 집합 $B$의 원소갯수가 3개 일떄는 i 이 성립하면 ii 는 자명!
(note2) 집합 $B$의 원소갯수가 4개 이상 일때는 무조건 일차종속 (기저가 될 수 없다)
** 집합 $B$의 원소갯수가 3개일 경우, 3개의 벡터가 일차독립이면 집합 $B$는 유클리드 (삼차원)공간의 기저이다.
sol) 벡터 $ a, b, c $가 일차독립이면 $ xa+yb+zc=0 $ 을 만족하는 $ x, y, z $ 는 $ x=y=z=0 $ 이다.
이때, $ a=(\: a_{1}, \: a_{2}, \: a_{3}\: ) $ ,$ b=(\: b_{1}, \: b_{2}, \: b_{3}\: ) $, $ c=(\: c_{1}, \: c_{2}, \: c_{3}\: ) $ 라고 하면
$$
\begin{matrix}
xa_{1}+yb_{1}+zc_{1}=0 \\
xa_{2}+yb_{2}+zc_{2}=0\\
xa_{3}+yb_{3}+zc_{3}=0
\end{matrix}
$$
이 성립한다.
즉, 유일한 해 $x=y=z=0$ 이 존재하려면
$$
det\begin{vmatrix}
a_{1} & b_{1} & c_{1}\\
a_{2} & b_{2} & c_{2}\\
a_{3} & b_{3} & c_{3}
\end{vmatrix}\neq 0
$$
$ \Rightarrow a,b,c $가 기저가 되기 위한 필요충분조건!!
이 말의 뜻을 해석해보면 $E^3$안의 임의의 벡터 $u= \begin{pmatrix}
u_{1} & u_{2} & u_{3}
\end{pmatrix} $ 에 대해서
$$
\left\{\begin{matrix}
u_{1}=xa_{1}+yb_{1}+zc_{1}\\
u_{2}=xa_{2}+yb_{2}+zc_{2}\\
u_{3}=xa_{3}+yb_{3}+zc_{3}
\end{matrix}\right.
$$
의 해가 존재한다고 생각할 수 있다. $\left ( x=k_{1},\: y=k_{2},\: z=k_{3} \right )$
즉, $E^3$안의 임의의 벡터 $u=k_{1}a+k_{2}b+k_{3}b$로 나타낼 수 있다.
$\therefore $일차결합으로 표시 가능하다.
**집합B의 원소갯수가 4개 이상일 경우에는 무조건 일차종속이다.(유클리드 (삼차원)공간의 기저가 될 수 없다)
sol) 집합 $B$의 원소 $u_{1},\: u_{2},\: u_{3},\: u_{4},\: \cdots ,\: u_{n}$ 중 $u_{1},\: u_{2},\: u_{3}$가 일차독립일 경우, $u_{1},\: u_{2},\: u_{3}$는 $E^3$의 기저가 되므로
집합 $B$의 또다른 원소 $ u_{4},\: \cdots ,\: u_{n}$은 $u_{1},\: u_{2},\: u_{3} $의 일차결합으로표현이가능하다.$ \left ( u_{4}=k_{1}u_{1}+k_{2}u_{2}+k_{3}u_{3} \right ) $
즉, $ k_{1}u_{1}+k_{2}u_{2}+k_{3}u_{3}+k_{4}u_{4}=0 $는 $0$이 아닌 해가 존재하므로 일차종속이다.
$\therefore $ 4개 이상의 원소를 가진 집합 $B$ 는 일차종속이므로 $E^3$의 기저가 될 수 없다.
(예제)

| 직교화 (0) | 2020.10.21 |
|---|---|
| 스칼라곱 (0) | 2020.10.14 |
| 일차종속, 일차독립 (0) | 2020.10.02 |
일차종속, 일차독립이란?

Ex1) 두 벡터가 평행이다. <=> 두 벡터는 일차종속이다.

Ex2) 영벡터를 포함하면 일차종속이다.

Ex3) 벡터 u1, u2, ... , un 이 종속이다. <=> 이 중 어느 한 벡터가 다른 것들의 일차결합이다.

Ex4) 일차종속인 부분집합을 포함하는 벡터의 집합은 일차종속이다.

Thm) 한 벡터가 일차독립인 벡터의 일차결합으로 표시된다면 그 표현법은 오직 하나다.
